
本文系用户投稿,不代表机核网观点
⚠️ 未经作者授权 禁止转载
压缩魔法
压缩魔法
在数码世界中,容量和速度总是紧缺资源,我们总是希望能用尽量少的字节,装下更多的内容;我们的硬盘总是不够用;我们的网络总是不够快。这一切,都需要使用一些数字魔法来帮助我们——压缩算法。
通用压缩算法原理
通用压缩算法原理
如何用尽量少的空间来存放尽量多的信息,这个问题一直是所有软件工程师都希望解决的。因此,首先有一些通用的压缩方法被提出来,虽然这些算法被应用的非常广泛,但是其原理确实非常简单的。我们常用的压缩软件,比如ZIP/RAR都会用到;我们上网的时候,传输的数据也大多数都经过压缩。
第一个要介绍的压缩方法叫RLF,说起来也很简单,其实就针对那些“连续重复”的信息做压缩。比方说有一串数字1,2,3,4,4,4,4,4,4,5,如果要压缩它,最容易发现的是这串数字中的数字4重复了很多遍,因此我们可以用0,4,6这三个数字来代表4,4,4,4,4,4,这里的0,4,6,表示的意思是:0-从这里开始有重复数字;4-这个是重复的数字;6-重复了6次。这样压缩之后的数字就是1,2,3,0,4,6,5这样一串数字。从10个数字就压缩成了7个数字,如果重复的内容越长,压缩率越高。这种依赖连续重复的算法是不是很简单呢?
第二个要介绍的方法叫哈夫曼算法,这个算法简单来说,就是查字典。举个例子,我如果要压缩一片文章,那么我可以找一本《现代汉语词典》,然后把文章中的每个词,都改写成它在《现代汉语词典》中的序号,最后改写完,把词典和文章一起打包就可以了。这种算法在我们的软件中使用的非常广泛,但是也有很大的缺点,就是那个压缩的词典可能会很大,因为文章中可能重复的词汇只有2处,但就需要占用一个词典中的条目,在压缩和解压的过程中,查询一个巨大的词典很耗费时间。
由于哈夫曼算法有上面的缺点,人们发明了另外一种算法,叫LZ77,这种算法改进了哈夫曼算法,它并不把整个压缩内容的词汇都编到一个词典里面。而是使用一段固定长度的词典,这段词典的内容就是刚刚处理被压缩后的原文。比如我们要压缩abcdbbccaa abaeaaabaee这样一串数字,前面的abcdbbccaa是已经被压缩处理过的文字,它们会用来作为处理后面字符的字典。当我们压缩abaeaaabaee的时候,我们发现第一个和第二字母ab是可以从字典abcdbbccaa中匹配到头两个字符的,所以就可以记录成:0,2,a。意思是匹配了字典的第0个字符后2个字符,匹配完的下个字符是a。后续的压缩就是不断的移动压缩的位置和字典的位置,就能形成一个压缩串,这个串既带了表示重复字符的数字,也包含了字典的内容,而字典则是固定长度的。这种算法的好处是压缩和解压的速度都比较快,如果要增加压缩比,就要增加字典的长度就可以了,是一种可以调节压缩比的算法。
通用压缩算法基本上都是一个原理,就是减少重复部分。思想其实是非常简单的,但是为了更好的识别出重复的部分,以及减少压缩、解压时间的消耗,使用了很多复杂的方法。
图形压缩
图形压缩
图形文件一直是数码产品中占用容量的大户。为了降低图像信息的占用空间,人们发明了很多种方法。我们使用图像文件时,会发现有JPG/GIF/BMP/PNG/TIFF等很多种格式,这些格式往往都是对图像进行压缩的不同方案。
图像压缩技术一般分为两类,一类是有损压缩,原理是利用人眼不够犀利的特性,把图像中不太容易被关注的部分的信息去掉。一类是无损压缩,原理是针对图像的数据特点,来对数字信息进行压缩。一般来说有损压缩会损失画质,但是却能大幅度降低图像占用的空间;无损压缩对于某些特定图像的压缩效果可能很好,比如卡通画,但是对于照片这种没有什么特点的图像压缩效果可能很差。
先说说有损压缩,最简单的做法,就是把附近几个差不多的颜色的点,全部改成同样一个颜色的点。这样本来需要多个不同数字来表示不同的颜色,就全部变成了一个颜色,这样重复的数字就变多了,容量自然就能变小了。——这个只是个最简单的思路,真正的有损压缩算法比如JPEG,并不是简单的抹平成一种颜色,而是通过一种算法,来修改靠近的一小片8x8个像素的图像的颜色,让这些颜色数值的重复率变高而得到的。
下面说说无损压缩。无损压缩其中一个最简单的做法就是使用“调色板”,思路和通用压缩算法中的“查字典”是一样的。也就是把整个图像中所有的颜色都抽取出来编上号,然后重复颜色的点就可以用这个简单的编号来代替,而不需要具体记录红蓝绿三种色点的深浅了。这种算法对于颜色简单的图像非常有效,比如卡通画往往最大色彩只有256种,这样调色板之需要256个数字,也就是一个字节就能装下了。每个点记录色彩从12个字节直接降到了1个字节。容量一下就减少了十二分一。
视频压缩
视频压缩
说到视频压缩,大家最熟悉的就是MPEG这个名次,我们以前看的VCD就是MPEG算法做压缩的。那么他的原理是什么呢?说起来也非常简单。其实就是2个方面的压缩:
一个是所谓空间相关性:视频是由很多帧画面组成的一个动画片,每一帧画面里面,每一行之间的图像,都有一定的重复,所以对一个单独的画面,我们可以发现大量的靠近的、重复内容的点,这些重复的内容可以用来压缩。这和图像压缩的原理是一样的。
另外一个是所谓时间相关性:我们看的画面,每一帧之间变化的部分其实往往不是那么大,比如一个人说话的视频,大部分都是嘴巴部分的画面在动,其他部分的不动,我们就可以只记录那些有变化的部分,而不需要把每帧画面都完整的记录下来,这也可以大大减少需要记录的数据量。我们在看VCD的时候,有时候会卡顿,看到一堆马赛克。这个时候如果细心观察,你会发现,马赛克的位置往往是画面有变化的部位,这就是压缩算法只记录了变化部分的一个证明啦。
加密魔法
加密魔法
加密这个行当,在计算机诞生之前就已经存在了数千年。第一代的计算机,就是为了破解密码而产生的。现代,加密算法又成为了互联网世界中安全的基石,可以说是最重要的算法之一。
福尔摩斯和跳舞小人
福尔摩斯和跳舞小人
《福尔摩斯》小说中曾经提到一个案子,内容说的是,有一天,一个人发现自己家里,到处被画上了很多跳舞小人,看的他毛骨悚然,于是请来了福尔摩斯破案。最后福尔摩斯看出了这些跳舞小人,其实是一段加密后的文字,每个小人都代表着一个字母。当福尔摩斯破解了这些小人的含义后,这些图画最后就能被解读成一段文字了。
其实这就是一种最简单的加密方法,又叫做罗马法加密。具体做法就是用一张不为人知的字母表(密码表),去改写现成的文字。由于拉丁文文字都是拼音文字,所以一张不大的密码表就可以用来改写任意的文字。罗马人是最早使用这种方法来加密军事情报的,他们的密码表当然不是这些怪模怪样的小人,而是一个打乱了顺序的罗马字母表。
举个例子,比如密码表中A对应正常字母表中F的位置,那么所有明文中的F都要写成A。解密的时候,再把密文中的A改写成F就可以看了。但是这种加密方法也很容易被破解,破解的方法叫做“词频分析法”,原理就是:在英文(或者其他拉丁语言)中,字母表中的各个字母的,在正常文章中,出现的频率是固定,比如大家都会发现字母S的频率出现很高,而Z的频率很低,因此我们可以通过统计密文中所有字符的频率,然后比对正常的字母的频率,从而猜出哪个密文字符是代表哪个明文字符。
为了改变加密字符的频率,后来的德国人发明了一种新的加密方法,就是动态的密码表,原理就是,每加密一个字符,密码表的顺序都会产生变化,一般变化是把密码表的顺序单向的增加。这样加密出来的每个字符,就算明文是一样的,其密文都可能不一样的。这种密文就无法简单的进行频率统计了。更有甚者还加上2套密码表嵌套使用,进一步打乱了字符的出现频率。
异或
异或
我们知道,计算机处理的是数字信息,但是说到加密,计算机又是如何使用一段“密码表”来加密一段明文的呢?其实也非常简单,就是用到“异或”这个二进制算法。简单来说,“异或”的运算规则就是:对于第一个数来说,如果碰到第二个数字0就不变,碰到1就翻转。
异或用来做加密非常简单,如果把运算的一个数作为明文,另外一个数作为密码表,那么异或的运算结果就是密文,反过来则是解密的过程。我们可以把明文切成和密码表一样长度的数字串,然后一段段和密码表做异或操作,就能得到加密串了。当然,这个过程中,你还可以加入如修改密码表(也是一串数字)的字符顺序这种变化,就能得到类似德国人的循环加密机的效果。
由于这种加密算法,在加密和解密的时候,使用的是同一份密码表,所以被叫做对称加密法,英文缩写叫DES。这也是计算机中最常见的一种加密方法。
不对称加密
不对称加密
对称加密算法有一个缺点,就是密码表一旦泄露,获得密码表的人就可以使用这份密码表,冒充加密人来制造、串改密文。在互联网世界里,串改的数据往往比泄露的数据更可怕,这意味着可以冒充别人的身份。
因此,人们又发明出了“不对称加密”的算法。这种算法的密码表是分两套的,一份叫“公钥”,一份叫“私钥”。其中“公钥”是用来解密的,而“私钥”是用来加密的。你通过“公钥”是很难猜测出“私钥”的。这样,一份用来解密的公钥,就能成为证明这份密文出处的证明。这也是现代互联网中应用最广的一种的加密算法,英文叫做RSA加密。
当我们需要加密传输的时候,我们使用不同的密码表来进行加解密,可以让密文在解密端是安全的,因为公钥被知道的话,也仅仅是能解读内容,而不能生成内容。比如我们需要远程控制一台计算机,我们发出的指令就无法被伪造和串改,这对于互联网远程安全有至关重要的作用。
其他数字魔法
其他数字魔法
数字隐身术:隐写
数字隐身术:隐写
我们在一些电视剧里面,往往会看到一些关于黑客的描述,比如一个普通的视频文件,经过特殊处理后,居然能出现一段隐藏的文字。就好像古老的谍战电影中,情报人员用特殊墨水来写信,需要用特殊的方法,比如泡水,才能看到内容。其实这种把信息隐藏起来的技术,在数码技术中,是非常容易做到的。最简单的是利用一种数字编码格式的去隐藏另外一种数字编码。比如我们可以把一段TXT文本编码数字,加到一张图片里面。如果这个图片的解像度非常高,这段TXT文本的数字,只是很不起眼的几个像素点而已。或者我们可以把一段文本信息的数字,变成某个视频点出现的频率,在一段视频里面,特定位置的点的变化频率更是难以用肉眼看到。可以说只要你了解一些数字编码规则,你都可以想办法隐藏一些信息。
数字封印术:校验
数字封印术:校验
在数字技术中,我们还可以通过一些算法,来检查数据在传输、存储的过程中有没有出错。最普通的做法就是所谓奇偶校验。比如我们在磁盘存放了0100 1100八个位的数字,我们可以发现1的个数是3个,是奇数,我们在记录0100 1100 1这九个数字到磁盘。最后的1表示前面八个位中,1的格式是奇数。如果我们读取的时候读到0100 1000 1这九个数字,发现前八位中1只有2个,是偶数,和最后的1所代表的含义对不上,就知道出错了,可能需要重新读取一次,或者提示用户磁盘坏了。
另外一种校验算法,也可以用来快速的判断一段数据是否相同。它就是大名鼎鼎的md5算法。这种算法可以把任意长度的数字,运算出固定的一串16字节长的一个数字。这个16字节的数字,代表了被运算的原文的摘要信息,如果原文有一个位不一样,这个运算的结果,都会有非常大的差别(一半以上的位翻转)。我们在下载了一个大文件之后,往往可以用md5来校验一下,和原来的文件的md5运算结果是否一致,就知道这个文件有没有在下载过程中出错了。一般来说,我们很难通过修改预算的原文,来凑出一个自己想要的md5运算结果,所以很长一段时间内md5被认为是“单向”的算法。但是2009年谢涛和冯登国仅用了220.96的碰撞算法复杂度,破解了MD5的碰撞抵抗,该攻击在普通计算机上运行只需要数秒钟。
无限变大术:矢量图
无限变大术:矢量图
一般来说,我们在存储图像的时候,都把图像分成很多个点,然后好像十字绣一样,拼成一个大的图像。但是这种图像在放大到一定程度之后,就看到一个个像素点,显得特别粗糙。因此有一些人另辟蹊径,他们在存储图像的时候,并不是拆分像素点,而是把图像中的线条,用数学公式来表达,创造出一种无论如何放大都不会“失真”的图像格式——矢量图格式。这种格式还有另外一个有点,就是容量大小也和解像度无关。不像一般的点阵图,解像度越大往往占用容量越大,而矢量图的容量大小仅仅和图像的线条复杂度有关,和解像度大小无关。因此在互联网上,矢量图和矢量动画更容易被下载,这也导致了FLASH格式的流行。
我们知道,数学函数是可以用图像来表达的,不同的函数可以构成不同弧度和变化的函数图像,而函数的内容本身,又可以控制函数图像的特征。因此,我们可以反过来,把图像“看成”是由一系列函数图像构成的,这样我们记录下这些函数,就能记录下图像本身了。而且由于函数本身和像素点无关,不过如何放大缩小(输入参数如何变化),图形都不会变化。
矢量图被广泛用于游戏、卡通片、LOGO设计、印刷出版等领域,由于不受分辨率影响,矢量图可以被完美的输出到各种媒介上。但是矢量图也有缺点,如果图像的轮廓线条非常复杂,比如照片,矢量图就需要大量复杂的数据结构才能表达,这导致了计算机处理能力的沉重负载。而且矢量图很难从类似照相机、扫描仪这类采集设备获得,基本上需要人工描画,这也让这种格式的图形难以被简单的使用。
这个系列到这里就结束了,虽然是科普系列,也是写了很久,感谢大家看到这里。如果有其他感兴趣的问题,欢迎留言,给我继续写这类文章提供一点启发。
I

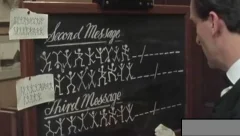



评论区
共 2 条评论热门最新